중력 상수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 뉴턴의 만유인력 법칙
- 2.2. 아인슈타인의 일반 상대성이론
3. 중력 상수의 측정
4. "GM" 곱 (표준 중력 변수)
- 4.1. 표준 중력 변수의 활용
- 4.2. 가우스 중력 상수
5. 플랑크 단위계
6. 중력 상수의 시간 불변성 (Constancy)
7. 중력 상수 값의 변천
8. 한국의 관점
참조

1. 개요

중력 상수는 만유인력의 법칙에서 두 물체 사이의 중력 크기를 결정하는 비례 상수이며, 아인슈타인의 일반 상대성 이론에도 등장한다. 헨리 캐번디시의 실험을 통해 처음으로 정교하게 측정되었으며, 중력은 다른 기본 상호작용에 비해 매우 약하고 측정의 어려움으로 인해 중력 상수의 정확도는 다른 물리 상수들에 비해 낮다. 중력 상수는 플랑크 단위계에서 1로 정의되며, 580개의 Ia형 초신성 관측을 분석한 결과 지난 90억 년 동안 거의 변하지 않은 것으로 나타났다.

더 읽어볼만한 페이지

물리 상수 - 보어 반지름
보어 반지름( $a_0$ )은 물리 상수들로 정의되며, 약 5.292 × 10^-11 m의 값을 가지고, 보어 모형에서 가장 안쪽 전자 궤도의 반지름으로 제시되어 원자 크기를 나타내는 척도로 사용된다.
물리 상수 - 볼츠만 상수
볼츠만 상수 k는 온도와 에너지를 연결하는 상수이며, 기체 상수와 아보가드로 상수의 비로 정의되고, SI 단위계에서 1.380649×10⁻²³ J/K의 값을 가지며, 거시 물리학과 미시 물리학을 연결하는 중요한 역할을 한다.
중력 - 중력 가속도
중력 가속도는 물체가 중력에 의해 가속되는 정도를 나타내는 값으로, 자유 낙하하는 물체의 가속도와 같으며, 지구의 경우 자전에 의한 원심력으로 인해 적도에서 가장 작고 극에서 가장 크게 나타난다.
중력 - 만유인력의 법칙
만유인력의 법칙은 모든 질량을 가진 물체들이 서로를 끌어당기는 힘에 대한 법칙으로, 뉴턴은 질량에 비례하고 거리의 제곱에 반비례한다는 것을 제시했으며, 케플러의 행성 운동 법칙을 설명하고 뉴턴 역학의 기초가 되었으나, 일반 상대성 이론이 등장하면서 저중력 한계로 여겨진다.

중력 상수
일반 정보
만유인력의 법칙에서의 만유인력 상수 G
기호	G
값	6.67430(15)×10⁻¹¹ m³ kg⁻¹ s⁻²
불확실성	2.2×10⁻⁵
정의	중력 상호작용의 크기를 나타내는 상수
영어 명칭	(Newtonian) constant of gravitation
상세 정보
공식	Fg = G (m₁m₂ / r²)
단위 (SI)	N m² kg⁻² = m³ kg⁻¹ s⁻²
기타 정보
가우스 인력 상수	가우스 인력 상수와 구별 필요

2. 정의

'''중력 상수'''(''G'')는 물리학에서 두 질량 사이에 작용하는 중력적 인력을 계산하는 데 사용되는 경험적인 물리 상수이다. 이 상수는 뉴턴의 만유인력 법칙과 아인슈타인의 일반 상대성 이론 모두에서 중요한 역할을 한다.

뉴턴의 만유인력 법칙에서 두 물체 사이의 중력적 인력(''F'')은 각 질량(''m''₁과 ''m''₂)의 곱에 정비례하고, 두 질량 사이의 거리(''r'')의 제곱에 반비례하는데, 이때 사용되는 비례 상수가 중력 상수 ''G''이다.

: $F = G \frac{m_1 m_2}{r^2}$

중력 상수는 종종 "큰 G"라고 불리며, 이는 지구 표면에서의 국소적인 중력 가속도를 나타내는 "작은 g"(''g'')와 구별하기 위함이다.^[1]^[2]

또한, 중력 상수는 일반 상대성 이론의 아인슈타인 장 방정식에도 나타난다.^[3]^[4]

: $G_{\mu \nu} + \Lambda g_{\mu \nu} = \kappa T_{\mu \nu} \,,$

여기서 ''G''_''μν''는 아인슈타인 텐서, Λ는 우주 상수, ''g''_''μν''는 계량 텐서, ''T''_''μν''는 응력-에너지 텐서이며, ''κ''는 아인슈타인 중력 상수이다. 아인슈타인 중력 상수 ''κ''는 뉴턴의 중력 상수 ''G''와 다음과 같은 관계를 가진다.^[4]^[5]

: $\kappa = \frac{8\pi G}{c^4} \approx 2.076647(46) \times 10^{-43} \mathrm{\,N^{-1}}.$

여기서 ''c''는 진공 중의 광속이다.

중력 상수의 2018년 CODATA 권장 값은 다음과 같다.^[48]

:''G'' = 6.67430(15)×10⁻¹¹ m³⋅kg⁻¹⋅s⁻²

괄호 안의 숫자는 표준 불확실성을 나타낸다. 이 값은 1kg의 두 질량이 1m 떨어져 있을 때 작용하는 인력이 약 6.67 × 10⁻¹¹ N임을 의미하며, 이는 매우 작은 힘이다.

또한, 중력 상수를 디랙 상수(ħ)와 진공 중의 광속(c)으로 환산한 무차원 양은 다음과 같다.^[49]

:''G''/ħ''c'' ≈ 6.70883(15)×10⁻³⁹ (GeV/''c''²)⁻²

2. 1. 뉴턴의 만유인력 법칙

만유인력의 법칙에 따르면, 두 물체 사이의 중력은 두 질량의 곱에 비례하며 거리의 제곱에 반비례한다. 이를 수식으로 나타내면 다음과 같다.

:

F = G \frac{m_1 m_2}{r^2}

이 식에서 비례 상수

G

를 '''중력 상수'''라고 부른다.

중력은 자연의 다른 세 상호작용에 비해 상대적으로 매우 약한 힘이다. 예를 들어, 각각의 질량이 3000 kg인 자동차 두 대가 질량 중심으로부터 3m 떨어져 있을 때, 두 자동차 사이에 작용하는 중력은 약 67 µ N에 불과하다. 이는 작은 모래 알갱이 하나의 무게와 비슷한 수준이다.

뉴턴의 만유인력 법칙은 구형 대칭 밀도 분포를 가진 두 물체 사이의 인력 힘의 크기 ''F''는 각 물체의 질량 ''m''₁과 ''m''₂의 곱에 정비례하고, 두 물체의 질량 중심 사이의 거리 ''r''의 제곱에 반비례함을 설명한다.

:

F=G\frac{m_1m_2}{r^2}

이 비상대론적 공식에서 비례 상수 ''G''는 중력 상수이다. 일반적으로 중력 상수는 "큰 G"라고도 불리며, 이는 지구 표면에서의 국소적인 중력장(자유 낙하 가속도라고도 함)을 나타내는 "작은 g" (''g'')와 구별하기 위함이다.^[1]^[2] 여기서

M_\oplus

는 지구의 질량이고

r_\oplus

는 지구 반지름이며, ''g''와 ''G''는 다음과 같은 관계를 가진다.

:

g = G\frac{M_\oplus}{r_\oplus^2}

2. 2. 아인슈타인의 일반 상대성이론

중력 상수는 일반 상대성 이론의 아인슈타인 장 방정식에 나타난다.^[3]^[4] 이 방정식은 시공간의 기하학적 구조와 그 안의 물질 및 에너지 분포 사이의 관계를 설명하며, 다음과 같이 표현된다.

G_{\mu\nu}+\Lambda g_{\mu\nu}=\frac{8\pi G}{c^4}T_{\mu\nu}

여기서 각 항은 다음과 같다.

$G_{\mu\nu}$ 는 아인슈타인 텐서로, 시공간의 곡률을 나타낸다. 이는 리치 텐서 $R_{\mu\nu}$ , 스칼라 곡률 $R$ , 그리고 계량 텐서 $g_{\mu\nu}$ 를 사용하여 $G_{\mu\nu} = R_{\mu\nu} - \frac{1}{2}Rg_{\mu\nu}$ 로 정의된다. (방정식 좌변의 $G_{\mu\nu}$ 는 중력 상수 ''G''와는 다른 물리량이다.)
$\Lambda$ 는 우주 상수이다.
$g_{\mu\nu}$ 는 시공간의 계량 텐서이다.
$T_{\mu\nu}$ 는 응력-에너지 텐서(또는 에너지-운동량 텐서)로, 물질과 에너지의 분포를 나타낸다.
$G$ 는 중력 상수이다.
$c$ 는 광속이다.

방정식 우변의 계수

\kappa = \frac{8\pi G}{c^4}

는 아인슈타인 중력 상수라고 불리며, 알베르트 아인슈타인이 처음 도입한 상수이다.^[4]^[5] 이 상수의 값은 대략 다음과 같다.

\kappa = \frac{8\pi G}{c^4} \approx 2.076647(46) \times 10^{-43} \mathrm{\,N^{-1}}

아인슈타인 중력 상수

\kappa

를 사용하면 아인슈타인 장 방정식은

G_{\mu \nu} + \Lambda g_{\mu \nu} = \kappa T_{\mu \nu}

로 간결하게 표현할 수도 있다.

3. 중력 상수의 측정

중력 상수는 1798년 헨리 캐번디시가 캐번디시 실험을 통해 처음으로 정밀하게 측정하였다.^[71]^[16] 캐번디시의 실험은 원래 지구의 질량을 측정하는 것이 목적이었으나, 이 실험을 통해 중력 상수의 값을 구할 수 있게 되었다.^[71]

그러나 중력 상수를 정확히 측정하는 것은 매우 어려운 일이다.^[6] 이는 중력이 다른 기본 힘들에 비해 극도로 약하고, 실험 과정에서 주변 다른 물체들의 중력 영향을 완벽히 차단하기 어렵기 때문이다.^[50] 또한 중력과 다른 힘들과의 알려진 관계가 없어 간접적인 측정 방법도 사용하기 어렵다. 이러한 이유로 중력 상수는 다른 중요한 물리 상수들에 비해 측정 불확실도가 매우 크다.^[50]^[51]^[52]

측정 기술의 발달로 정확도는 점차 향상되어 왔지만, 여전히 측정값들 사이에 불일치가 나타나기도 한다.^[6]^[30] CODATA는 주기적으로 최신 측정 결과들을 종합하여 중력 상수의 권장값을 발표하는데, 2018년 기준 권장값은 다음과 같다.^[48]

: ''G'' = 6.674 30(15) × 10^-11 m³⋅kg^-1⋅s^-2

이 값의 상대 측정 불확실도는 2.2 × 10^-5 (22 ppm)이다.^[48] 이는 질량 1kg인 두 물체가 1m 떨어져 있을 때 서로에게 작용하는 인력이 약 6.674 × 10^-11 N 정도로 매우 작다는 것을 의미한다. 예를 들어, 각각 1톤 (=1000kg) 무게의 물체가 1m 떨어져 있을 때 작용하는 인력은 약 6.7 × 10^-5 N 정도로, 지구상에서 약 6.8mg 질량의 물체에 작용하는 중력과 비슷하다.

중력 상수의 낮은 측정 정밀도는 쌍성 펄서의 질량 측정 정확도 등 다른 물리량 계산에도 영향을 미친다. 또한 mm 이하의 매우 작은 거리에서는 뉴턴의 만유인력 법칙이 아직 정밀하게 검증되지 않았기 때문에, 이 영역에서 중력 이론의 수정 가능성(예: 여분 차원을 포함하는 브레인 월드 모델 등)에 대한 연구가 활발히 진행되고 있다.

3. 1. 초기 측정

중력 상수의 존재는 1680년대에 출판된 뉴턴의 만유인력의 법칙에서 암시되었으나,

G

라는 기호로 표기되기 시작한 것은 1890년대부터이다.^[15] 뉴턴은 그의 저서 ''프린키피아''에서 중력의 역제곱 법칙을 가정했지만, 중력 상수의 값을 직접 계산하지는 않았다. 그는 큰 언덕 근처에서 진자의 흔들림을 측정하여 중력의 세기를 재려고 했으나, 그 효과가 너무 미미하여 당시 기술로는 측정할 수 없을 것이라고 생각했다.^[11] 그럼에도 뉴턴은 지구의 평균 밀도가 물의 5~6배 정도 될 것이라고 추측하며 상수의 크기를 어림했는데, 이는 대략

G \approx 6.7 \times 10^{-11} \, \text{m}^3 \text{kg}^{-1} \text{s}^{-2}

에 해당한다.^[12]

1738년, 피에르 부게와 샤를마리 드 라 콩다민은 페루 원정 중에 중력 상수를 측정하려는 시도를 했다. 부게는 1740년 그들의 실험 결과가 지구가 에드먼드 핼리 등이 주장했던 것처럼 속이 빈 껍질이 아님을 증명했다고 밝혔지만, 측정 자체의 중요성은 크지 않다고 평가했다.^[13]

지구의 평균 밀도를 성공적으로 측정한 첫 실험은 1772년에 제안되어 1776년에 완료된 스키핼리언 실험이다. 이 실험은 간접적으로 중력 상수를 측정한 것이기도 하다. 찰스 허턴이 1778년에 보고한 결과에 따르면 지구의 평균 밀도는 약 4.5 g/cm³ (물 밀도의 4.5배)로, 이는 현대 측정값보다 약 20% 낮은 수치였다.^[14] 이 결과를 바탕으로 허턴은 태양, 달, 행성들의 밀도와 질량을 추정하여 제롬 랄랑드에게 제공했다. 지구의 평균 반지름(

R_\oplus

)과 표면에서의 평균 중력 가속도(

g

)를 알면, 평균 밀도(

\rho_\oplus

)를 통해 다음과 같이 중력 상수(

G

)를 계산할 수 있다.^[15]

G = g\frac{R_\oplus^2}{M_\oplus} = \frac{3g}{4\pi R_\oplus\rho_\oplus}

허턴의 1778년 결과를 이 식에 적용하면

G \approx 8 \times 10^{-11} \, \text{m}^3 \text{kg}^{-1} \text{s}^{-2}

정도가 된다.

1798년 헨리 캐번디시가 G를 측정하기 위해 수행한 캐번디시 실험의 비틀림 저울 구조도. 도르래의 도움으로 프레임에 매달린 큰 공(W)을 작은 공(x) 옆에 놓는 방식으로 회전시켰다.

두 물체 사이의 중력 인력을 실험실에서 직접 측정한 최초의 실험은 뉴턴 사후 71년이 지난 1798년, 헨리 캐번디시에 의해 이루어졌다.^[16] 그는 지질학자 존 미첼이 1753년에 고안한 비틀림 저울을 사용하여 중력 상수를 정밀하게 측정했다.^[71] 이 장치는 수평 막대 양 끝에 작은 납 공을 매달고 비틀림에 민감한 줄에 연결한 형태이다. 막대의 진동 주기를 측정하여 관성 모멘트(비틀림 상수)를 알아낸 뒤, 큰 납 공을 작은 공 근처에 두었을 때 중력으로 인해 막대가 미세하게 회전하는 각도를 측정하여 두 공 사이의 인력을 계산했다. 이 실험은 미첼이 설계했지만 캐번디시가 성공적으로 수행했기 때문에 캐번디시 실험으로 불린다.

캐번디시의 주된 목표는 "지구의 무게를 재는 것", 즉 지구의 평균 밀도와 지구의 질량을 알아내는 것이었다. 그의 실험 결과, 지구의 평균 밀도는

\rho_{\oplus} = 5.448(33) \, \text{g/cm}^3

으로 측정되었고, 이는 중력 상수

G = 6.74(4) \times 10^{-11} \, \text{m}^3 \text{kg}^{-1} \text{s}^{-2}

값에 해당한다. 이 값은 현대의 측정값과 비교했을 때 약 1% 정도의 오차만을 가지는 놀랍도록 정확한 결과였다.^[17] 캐번디시 실험을 통해 중력 상수가 구해지면서, 이미 알려져 있던 지구 반지름과 중력 가속도 값을 이용해 지구의 질량과 밀도를 처음으로 계산할 수 있게 되었다. 이 실험에서 구한 만유인력 상수는 6.74 × 10⁻¹¹ m³ kg⁻¹ s⁻²였으며, 현재 알려진 값과 비교해도 상당히 정밀한 것이었다.

3. 2. 측정의 어려움

중력 상수는 높은 정확도로 측정하기 어려운 물리 상수이다.^[6] 이는 중력이 실험실 규모에서 다른 기본 힘에 비해 극도로 약한 힘이기 때문이다. 예를 들어, 1m 떨어진 전자와 양성자 사이의 중력은 대략 10^-67 N인데 반해, 동일한 두 입자 사이의 전자기력은 대략 10^-28 N이다. 이 예시에서 전자기력은 중력보다 약 10³⁹배 더 크다.

중력 상수의 측정은 헨리 캐번디시가 캐번디시 실험을 통해 정교하게 처음으로 측정한 이후^[71] 점차 정확도가 향상되어 왔지만, 그 개선 정도는 미미하다.^[18] 중력이 다른 기본 상호 작용에 비해 매우 약하고, 다른 물체의 중력적 영향을 정전 차폐와 같은 방법으로 제거하기 어렵기 때문에^[50] 중력 상수 ''G''를 측정하는 것은 여러 이유로 어렵다.^[6] 실험 장치를 주변 물질의 영향으로부터 완벽히 분리하는 것이 불가능하며,^[18] 중력과 다른 상호 작용 사이에 알려진 상관 관계가 없어 간접적으로 측정할 수도 없다.

이러한 어려움 때문에 중력 상수의 측정값은 시간이 지남에 따라 크게 변동해 왔으며, 최근의 몇몇 측정값들은 서로 일치하지 않는 경우도 있다. 초기 프란체스코 카를리니(1821), 에드워드 세빈(1827), 카를로 이그나치오 줄리오(1841), 조지 비델 에어리(1854) 등의 진자 실험 결과^[19]나 페르디난트 라이히(1838, 1842, 1853)의 캐번디시 실험 반복 결과^[20] 등은 현대 값과 상당한 차이를 보였다. 이후 존 헨리 포인팅(1891),^[23] C. V. 보이스(1895),^[24] 카를 브라운(1897)^[24] 등의 노력을 통해 측정 정확도가 개선되었지만, 여전히 다른 기본 상수에 비해 불확실성이 매우 크다.

SI 단위에서, CODATA가 권장하는 2018년 기준 중력 상수의 값은 다음과 같다.

: ''G'' = 6.674 30(15) × 10^-11 m³·kg^-1·s^-2

이 값의 상대 측정 불확실도는 2.2 × 10^-5 (또는 22 ppm)이다. 이는 다른 중요한 물리 상수들에 비해 매우 높은 불확실성이며,^[50]^[51]^[52] 값의 가수 부분인 6.67까지만 어느 정도 확정적이라고 볼 수 있다. 이처럼 정밀도가 낮기 때문에 CODATA 권장값 역시 시대에 따라 계속 변해왔다.^[53]

만유인력 상수의 CODATA 권장값 변천^[54]
	권장값 G (10^-11·m³·kg^-1·s^-2)	상대 표준 불확정성
1973 CODATA^[55]	6.6720(41)	6.1 × 10^-4
1986 CODATA	6.672 59(85)	1.3 × 10^-4
1998 CODATA	6.673(10)	1.5 × 10^-3
2002 CODATA	6.6742(10)	1.5 × 10^-4
2006 CODATA	6.674 28(67)	1.0 × 10^-4
2010 CODATA	6.673 84(80)	1.2 × 10^-4
2014 CODATA	6.674 08(31)	4.7 × 10^-5
2018 CODATA	6.674 30(15)	2.2 × 10^-5

만유인력 상수의 낮은 측정 정밀도는 쌍성 펄서의 질량 측정 정확도 등 다른 물리량 측정에도 영향을 미친다. 또한, 밀리미터 이하의 매우 작은 거리(μm, nm 등)에서는 뉴턴의 만유인력 법칙이 아직 정밀하게 검증되지 않았기 때문에, 이 영역에서 중력 이론의 수정 가능성, 예를 들어 여분 차원을 포함하는 브레인 월드와 같은 새로운 이론 모델에 대한 연구가 활발히 진행되고 있다.

3. 3. 현대적 측정값과 불확실성

중력 상수는 높은 정확도로 측정하기 어려운 물리 상수이다.^[6] 이는 중력이 실험실 규모에서 다른 기본 힘에 비해 극도로 약한 힘이기 때문이다. 또한 중력은 다른 물체의 영향을 쉽게 받으며, 다른 상호작용과의 알려진 관계가 없어 간접적인 측정 또한 불가능하다. 이러한 이유로 중력 상수의 측정값은 역사적으로 상당한 변동을 보여왔으며, 최근의 정밀 측정값들 사이에서도 서로 일치하지 않는 경우가 보고되었다.^[6]^[30]

헨리 캐번디시의 실험 이후 중력 상수의 측정 정확도는 점차 향상되었지만, 그 과정은 순탄치 않았다. 예를 들어, 폴 R. 헤일은 1930년에 6.670(5) × 10⁻¹¹ m³⋅kg⁻¹⋅s⁻² (상대 불확실도 0.1%)^[28], 1942년에는 6.673(3) × 10⁻¹¹ m³⋅kg⁻¹⋅s⁻² (상대 불확실도 0.045% = 450 ppm)로 개선된 값을 발표했지만,^[29] 측정에 사용된 재료에 따라 결과가 달라지는 문제를 해결하지 못했다.

1950년대 이후 발표된 측정값들은 헤일의 값과 대체로 일치했지만, 상대 불확실도는 약 0.1% (1000 ppm) 내에서 변동했으며, 1980년대부터 2000년대 사이에는 서로 모순되는 측정 결과들이 발표되기도 했다.^[6]^[30] 이로 인해 0.1% 미만의 상대 표준 불확실도를 가진 표준값을 설정하는 것은 오랫동안 어려운 과제로 남아 있었다.

NIST가 권장하는 값의 불확실도는 1969년 460 ppm에서 1986년 120 ppm으로 감소했으나, 측정값들의 불일치로 인해 1998년에는 불확실도를 1500 ppm (0.15%)으로 다시 크게 높였다. 이후 불확실도는 점차 감소하여 2014년에는 46 ppm까지 낮아졌고, 2018년에는 22 ppm으로 더욱 개선되었다.^[31]^[39]^[40]

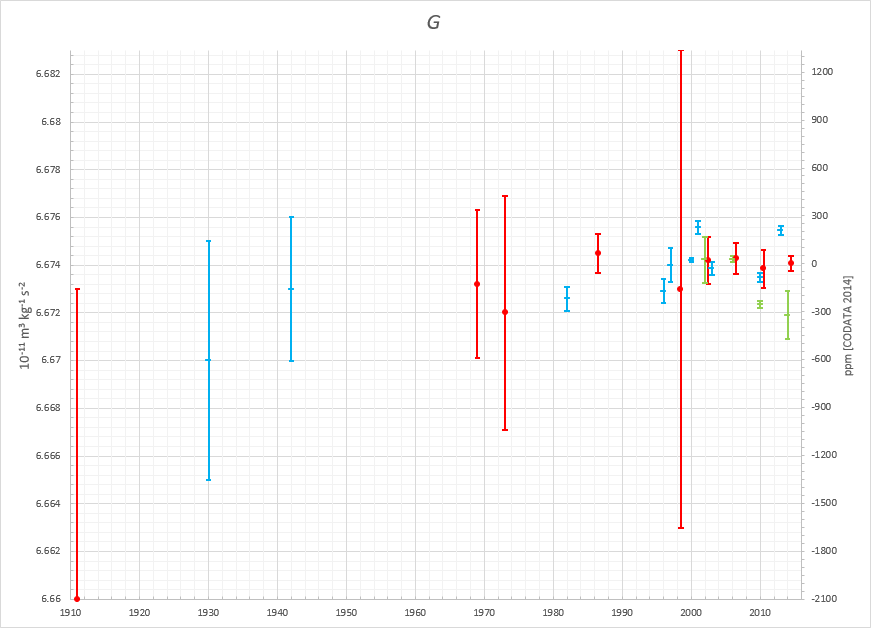
1900년 이후 ''G''의 측정 및 권장 값의 타임라인: 문헌 검토를 기반으로 권장되는 값은 빨간색, 개별 비틀림 균형 실험은 파란색, 기타 유형의 실험은 녹색으로 표시.

다음 표는 1969년 이후 CODATA와 NIST에서 권장하는 중력 상수 값의 변화를 보여준다. CODATA 권장값은 국제적으로 널리 사용되는 표준값이다.

''G''에 대한 CODATA 권장값 변천^[54]
	권장값 G (10⁻¹¹ m³⋅kg⁻¹⋅s⁻²)	상대 표준 불확실도
1973 CODATA^[55]	6.6720(41)	610 ppm
1986 CODATA	6.67259(85)	130 ppm
1998 CODATA	6.673(10)	1500 ppm
2002 CODATA	6.6742(10)	150 ppm
2006 CODATA	6.67428(67)	100 ppm
2010 CODATA	6.67384(80)	120 ppm
2014 CODATA	6.67408(31)	47 ppm
2018 CODATA	6.67430(15)	22 ppm

''G''에 대한 NIST 권장값 변천
연도	G (10⁻¹¹ m³⋅kg⁻¹⋅s⁻²)	상대 표준 불확실도	참고
1969	6.6732(31)	460 ppm	^[32]^[56]
1973	6.6720(49)	730 ppm	^[33]^[57]
1986	6.67449(81)	120 ppm	^[34]^[58]
1998	6.673(10)	1500 ppm	^[35]^[59]
2002	6.6742(10)	150 ppm	^[36]^[60]
2006	6.67428(67)	100 ppm	^[37]^[61]
2010	6.67384(80)	120 ppm	^[38]^[62]
2014	6.67408(31)	46 ppm	^[39]^[63]
2018	6.67430(15)	22 ppm	^[40]^[64]
2022	6.67430(15)	22 ppm	^[41]

최근에는 원자 간섭계와 같은 새로운 기술을 이용한 측정 시도도 이루어지고 있다. 2007년 ''사이언스''에 발표된 픽슬러 등의 연구에서는 원자 간섭계를 이용하여 ''G'' = 6.693(34) × 10⁻¹¹ m³⋅kg⁻¹⋅s⁻² 라는 값을 보고했는데, 이는 당시 CODATA 값보다 0.28% (2800 ppm) 높은 값이었다.^[42]^[67] 2014년 로시 등은 개선된 냉원자 측정을 통해 ''G'' = 6.67191(99) × 10⁻¹¹ m³⋅kg⁻¹⋅s⁻² 로 발표했다.^[43]^[44] 이 값은 기존 권장값에 더 가깝지만, 2014년 CODATA 권장값과는 여전히 불확실도 구간이 겹치지 않는 차이를 보였다.

2018년 현재, 상충되는 측정 결과에 대한 재평가를 위한 노력이 NIST의 조정 하에 진행 중이다.^[45]

2018년 8월, 중국 연구팀은 비틀림 저울을 이용한 두 가지 다른 방법으로 측정한 결과로 각각 6.674184(78) × 10⁻¹¹ m³⋅kg⁻¹⋅s⁻² 및 6.674484(78) × 10⁻¹¹ m³⋅kg⁻¹⋅s⁻² 를 발표했다.^[46] 이 측정들은 12 ppm이라는 매우 낮은 상대 표준 불확실도를 주장했지만, 두 결과값 사이의 차이(2.7''σ'')는 아직 설명되지 않은 오차 요인이 있을 가능성을 시사한다.

현재 CODATA가 권장하는 2018년 중력 상수 값은 다음과 같다.^[48]

: ''G'' = 6.67430(15) × 10⁻¹¹ m³⋅kg⁻¹⋅s⁻²

괄호 안의 숫자는 마지막 자릿수의 표준 불확실성을 나타낸다. 이 값은 질량 1 kg인 두 물체가 1 m 떨어져 있을 때 작용하는 인력이 약 6.674 × 10⁻¹¹ N임을 의미하며, 이는 매우 작은 힘이다. 예를 들어, 각각 1톤(=)인 물체가 1 m 떨어져 있을 때 서로 끌어당기는 힘은 약 6.7 × 10⁻⁵ N으로, 지구상에서 약 6.8 mg 질량의 물체에 작용하는 중력과 비슷하다.

중력 상수를 디랙 상수(ħ)와 진공 속 빛의 속도(c)로 환산한 값은 다음과 같다.^[49]

: ''G'' / (ħc) ≈ 6.70883(15) × 10⁻³⁹ (GeV/''c''²)⁻²

이처럼 중력 상수의 측정값은 다른 물리 상수에 비해 불확실성이 매우 크다 (상대 표준 불확실도 22 ppm).^[50]^[51]^[52] 값의 유효 숫자가 소수점 이하 두 자리(6.67) 정도까지만 확실하며, 이는 CODATA 권장값이 시대에 따라 크게 변동하는 원인이 된다.^[53] 예를 들어, 2018년 권장값과 2014년 권장값의 차이는 3.3×10^-5로, 기초 물리 상수로서는 매우 큰 변화이다.

이러한 낮은 정밀도는 쌍성 펄서의 질량 측정 정확도 등에 영향을 미친다. 또한 밀리미터 이하의 짧은 거리에서는 뉴턴의 만유인력 법칙이 정밀하게 검증되지 않았기 때문에, 작은 규모에서는 중력 이론의 수정 가능성(예: 여분 차원을 포함하는 브레인 월드 모델)이 연구되고 있다.

한편, 국제 측지학 협회(IAG)는 1999년에 ''G'' = 6.67259(30) × 10⁻¹¹ m³⋅kg⁻¹⋅s⁻² 값을 사용하기로 결정했으며,^[65] NASA도 이 값을 채택하고 있다.^[66]

4. "GM" 곱 (표준 중력 변수)

중력 상수 $G$ 와 특정 천체의 질량 $M$ 의 곱인 $GM$ 은 표준 중력 변수( $\mu$ 로도 표기)라고 하며, 여러 중력 관련 수식을 단순화하는 데 유용하게 사용된다. 특히 태양계 천체들의 운동을 뉴턴의 만유인력 법칙으로 기술할 때, 개별적인 $G$ 값이나 $M$ 값보다 그 곱인 $GM$ 값을 훨씬 높은 정확도로 측정할 수 있기 때문에 빈번하게 활용된다.^[9]^[10]

중력 상수 $G$ 자체의 측정 정밀도는 상대적으로 낮지만, 행성의 위치나 표면에서의 중력 가속도와 같은 관측 가능한 양들은 매우 정밀하게 측정될 수 있다. 이러한 관측값들은 $G$ 와 $M$ 의 곱인 $GM$ 에 의존하므로, 결과적으로 $GM$ 값은 매우 정확하게 결정될 수 있다. 예를 들어, 지구나 태양의 표준 중력 변수 값( $GM_\mathrm{Earth}$ , $GM_\odot$ )은 매우 높은 정밀도로 알려져 있다.^[9]^[10]

이처럼 $GM$ 값이 $G$ 나 $M$ 각각보다 훨씬 정확하게 알려져 있기 때문에, 천체 역학의 많은 계산에서는 $G$ 와 $M$ 을 분리하지 않고 $GM$ 값을 하나의 상수로 사용하여 계산의 전체적인 정확도를 높인다. 역으로 말하면, 지구 질량( $M_\mathrm{Earth}$ )이나 태양 질량( $M_\odot$ )의 측정값의 정확도는 현재까지 알려진 중력 상수 $G$ 의 정확도에 의해 제한된다.^[68]^[69]

4. 1. 표준 중력 변수의 활용

GM

곱 또는 표준 중력 변수는 여러 가지 중력과 관계된 수식을 간단히 표현하는 데 자주 활용된다. 특히 태양계에 대해 중력 법칙을 이용할 때 매우 높은 정확도로 측정할 수 있기 때문에 빈번하게 사용된다. 중력 상수

G

의 정확도가 높지 않은 데 반해 행성의 위치나 중력 가속도와 같은 양은 매우 정확하게 측정할 수 있다. 따라서 중력 상수와 질량의 곱

GM

은 매우 정확하게 알아낼 수 있다(따라서 지구나 태양의 질량 측정값의 정확도는 중력 상수

G

의 정확도에 의존한다). 태양계에서의 중력을 계산할 때 거의 대부분의 계산에서

GM

값이 함께 붙어서 나오며, 대부분의 계산에서 이 둘을 따로 대입할 필요가 없어 정확도를 높일 수 있다.

지구의 표준 중력 변수(

\mu = GM

) 값은 국제단위계(SI)에서 다음과 같은 값을 갖는다.

\mu = GM = (3.986004418 \pm 0.000000008) \times 10^{14} \, \mathrm{m^3 s^{-2}}

이는 약

398,600.4418 \, \mathrm{km^3 s^{-2}}

에 해당한다.

천체 역학에서는 주로 국제단위계의 킬로그램보다 태양 질량(

M_\odot

)을 기준으로 한 단위계를 사용하는 것이 계산에 편하다. 이 단위계로 쓴 중력 상수를 '''Gaussian gravitational constant|가우스 중력 상수^영어'''

k

라 부르며, 그 값은 다음과 같다.

k = 0.01720209895 \, A^{3/2} D^{-1} S^{-1/2}

여기서

A

는 천문 단위,

D

는 평균 태양일, 그리고

S

는 태양 질량이다. 이 상수는 태양-지구 시스템의 평균 각속도를 나타내며 약

0.0172

라디안/일이다. 그러나 이 상수와 관련된 천문 단위의 정의는 2012년부터 국제 천문 연맹(IAU)에 의해 폐지되었다.

천체물리학에서는 거리를 파섹(pc), 속도를 초당 킬로미터(km/s), 질량을 태양 단위

M_\odot

로 측정하는 것이 편리하다. 이러한 단위에서 중력 상수는 다음과 같다.

G \approx 4.3009 \times 10^{-3} \, \mathrm{pc \cdot (km/s)^2} \, M_\odot^{-1}

조석이 중요한 상황에서는 관련 길이 척도가 파섹이 아닌 태양 반지름(

R_\odot

)이다. 이러한 단위에서 중력 상수는 다음과 같다.

G \approx 1.90809 \times 10^{5} \, \mathrm{R_\odot \cdot (km/s)^2} \, M_\odot^{-1}

궤도 역학에서 질량이

M

인 구형 물체를 중심으로 하는 원형 궤도에서 물체의 주기

P

는 궤도 반지름

r

과 다음 관계를 따른다.

GM = \frac{4\pi^2 r^3}{P^2}

만약 궤도 반지름 내부의 부피를

V = \frac{4}{3}\pi r^3

라고 하면, 위 식은 다음과 같이 표현될 수도 있다.

GM = \frac{3\pi V}{P^2}

이

G

를 표현하는 방식은 행성의 평균 밀도와 그 표면 바로 위를 공전하는 위성의 주기 사이의 관계를 보여준다.

케플러의 3법칙을 적용하여 타원 궤도의 경우 지구 궤도를 특징짓는 단위(천문 단위 AU, 태양년 yr, 총 질량

M

)로 표현하면 다음과 같다.

G = 4 \pi^2 \, \mathrm{AU^3 yr^{-2}} \, M^{-1} \approx 39.478 \, \mathrm{AU^3 yr^{-2}} \, M_\odot^{-1}

여기서 거리는 지구 궤도의 장반경(천문 단위, AU)으로 측정하고, 시간은 태양년으로, 질량은 공전하는 시스템의 총 질량(

M = M_\odot + M_\oplus + M_L

등)이다. 위의 방정식은 뉴턴 역학에서 태양 주위를 공전하는 지구 궤도를 두 물체 문제로 근사하는 경우에만 정확하며, 측정된 양은 태양계의 다른 물체로부터의 섭동 및 일반 상대성 이론의 보정을 포함한다.

그러나 1964년부터 2012년까지 천문 단위의 정의로 사용되었으므로 정의상 유지되었다.

1 \, \mathrm{AU} = \left( \frac{GM_\odot}{4 \pi^2} \mathrm{yr}^2 \right)^{1/3} \approx 1.495979 \times 10^{11} \, \mathrm{m}

2012년부터 AU는 정확히

1.495978707 \times 10^{11} \, \mathrm{m}

로 정의되며, 더 이상 방정식을 정확하게 유지할 수 없다.

중력 상수와 태양 또는 지구와 같은 주어진 천체의 질량의 곱인

GM

은 표준 중력 변수(

\mu

로도 표시됨)로 알려져 있다. 표준 중력 변수

GM

은 뉴턴의 만유인력 법칙, 중력 렌즈로 인한 빛의 굴절 공식, 케플러의 행성 운동 법칙, 탈출 속도 공식에 나타난다. 이 양은 다양한 중력 관련 공식의 편리한 단순화를 제공한다. 곱

GM

은 각 인자(

G

와

M

)보다 훨씬 더 정확하게 알려져 있다.

''GM'' 값
물체	$\mu = GM$	값 ( $\mathrm{m^3 s^{-2}}$ )	상대 불확실성
태양	$GM_\odot$	$1.32712440018(8) \times 10^{20}$ ^[9]	$6 \times 10^{-11}$
지구	$GM_\oplus$	$3.986004418(8) \times 10^{14}$ ^[10]	$2 \times 10^{-9}$

만유인력 상수 측정 정밀도가 낮은 것에 비해, $G$ 에 태양 질량 $M_\odot$ 을 곱한 '''태양중력상수'''( $GM_\odot$ )나, 지구 질량 $M_\oplus$ 를 곱한 '''지구중력상수'''( $GM_\oplus$ )는 위 표와 같이 정밀하게 측정되고 있다.^[68]

따라서, 지구 질량의 정밀도는 만유인력 상수 측정 정밀도에 의존하며, CODATA 2006에 따른 지구 질량은 $M_\oplus = (5.9722 \pm 0.0006) \times 10^{24} \, \mathrm{kg}$ 로 계산되었고^[68], 국제 측지학 협회(IAG)의 협정값에서는 $M_\oplus = (5.9737 \pm 0.0003) \times 10^{24} \, \mathrm{kg}$ 로 계산된다. NASA에서는 $M_\oplus = 5.9736 \times 10^{24} \, \mathrm{kg}$ 로 하고 있다^[69].

4. 2. 가우스 중력 상수

천체 역학에서는 계산의 편의를 위해 국제단위계의 킬로그램(kg) 대신 태양 질량(

M

_⊙)을 기준으로 한 단위계를 사용하는 경우가 많다. 이 단위계에서 정의된 중력 상수를 '''가우스 중력 상수'''(Gaussian gravitational constant|가우스 중력 상수^eng)라고 부르며, 기호로는

k^2

를 사용한다. 가우스 중력 상수

k

의 값은 다음과 같다.

:

k = 0.01720209895 \ A^{\frac{3}{2}} \ D^{-1} \ S^{-\frac{1}{2}}

여기서

A

는 천문 단위(AU),

D

는 평균 태양일,

S

는 태양 질량을 의미한다.

역사적으로 천체 역학 계산 시 표준 SI 단위 대신 태양 질량, 평균 태양일, 천문 단위를 사용하는 경우가 많았고, 이때 가우스 중력 상수가 널리 활용되었다. 상수 값

k = 0.01720209895

라디안/일은 태양-지구 시스템의 평균 각속도를 나타낸다. 그러나 가우스 중력 상수와 과거 천문 단위의 정의 방식은 2012년 국제천문연맹(IAU) 총회 결정을 통해 더 이상 사용되지 않게 되었다.

5. 플랑크 단위계

중력 상수 ''G''는 플랑크 상수 ''ħ''와 빛의 속도 ''c''와 함께 막스 플랑크의 이름을 따서 플랑크 단위계를 정의하는 데 사용된다. 플랑크 단위계는 임의적인 기본 단위 없이 물리 상수만으로 정의되는 단위계이다. 이 단위계에서 중력 상수 ''G'', 플랑크 상수 ''ħ'', 그리고 진공에서의 빛의 속도 ''c''의 값은 모두 1로 설정된다.

중력 상수는 자연 단위계의 정의 상수로서 중요한 역할을 한다.^[7]^[8] 특히 플랑크 단위계나 스토니 단위계와 같은 기하학적 단위계에서 중력 상수의 값은 해당 단위로 표현될 때 일반적으로 1 또는 그에 가까운 값을 가진다. 그러나 다른 기본 상수들에 비해 중력 상수 ''G''의 측정값은 상당한 불확실성을 가지고 있다. 이 때문에 플랑크 단위계와 같은 단위계로 표현되는 다른 많은 물리량의 값에도 비슷한 수준의 불확실성이 나타나게 된다.

6. 중력 상수의 시간 불변성 (Constancy)

580개의 Ia형 초신성 관측 분석 결과에 따르면 중력 상수는 지난 90억 년 동안 1년에 100억 분의 1 미만으로 변화했다.^[47]

7. 중력 상수 값의 변천

폴 R. 헤일은 1930년에 ''G'' = 6.670(5)×10⁻¹¹ m³⋅kg⁻¹⋅s⁻² (상대 불확실도 0.1%) 값을 발표했고,^[28] 1942년에는 ''G'' = 6.673(3)×10⁻¹¹ m³⋅kg⁻¹⋅s⁻² (상대 불확실도 0.045%, 450 ppm)로 개선된 값을 제시했다.^[29] 그러나 헤일 자신도 동일한 재료를 사용한 측정에서는 결과가 매우 유사했지만, 다른 재료를 사용하면 결과가 크게 달라진다는 점을 인정했다. 그는 재료 조성에 따른 효과가 사라지기를 바라며 12년간 더 정확한 측정을 수행했지만, 1942년 마지막 논문에서 언급했듯이 그렇지 않았다.

1950년대 이후 고정밀 측정에서 발표된 ''G'' 값들은 헤일 (1930)의 값과 대체로 일치했지만, 상대 불확실도가 약 0.1% (1000 ppm) 범위 내에서 상당히 넓게 변동했다. 1942년 측정 이후 불확실도가 실제로 감소했는지조차 명확하지 않았다. 1980년대부터 2000년대 사이에 발표된 일부 측정값들은 서로 상충되기까지 했다.^[6]^[30] 이 때문에 상대 표준 불확실도가 0.1% 미만인 ''G''의 표준 값을 설정하는 것은 여전히 어려운 문제로 남아 있다.

1969년 국립표준기술연구소(NIST)에서 권장하는 값은 상대 표준 불확실도가 0.046% (460 ppm)였고, 1986년에는 0.012% (120 ppm)까지 낮아졌다. 그러나 상충되는 측정값들이 계속 발표되면서, NIST는 1998년 권장 값에서 표준 불확실도를 이전보다 12배나 큰 0.15% (1500 ppm)로 높여야 했다. 이는 헤일 (1930)이 제시한 불확실성보다도 큰 값이었다.

불확실성은 2002년과 2006년에 다시 낮아졌지만, 2010년에는 다시 보수적으로 20% 증가하여 1986년의 상대 표준 불확실도(120 ppm)와 같아졌다.^[31] 2014년 업데이트에서는 CODATA가 불확실성을 46 ppm으로 줄였는데, 이는 2010년 값의 절반 미만이며 1969년 권고안보다 한 자릿수 낮은 값이다.

아래 표는 1969년 이후 발표된 NIST 권장 값을 보여준다.

''G''에 대한 권장 값
연도	G (10⁻¹¹ m³⋅kg⁻¹⋅s⁻²)	상대 표준 불확실도	참고
1969	6.6732(31)	460 ppm	^[32]
1973	6.6720(49)	730 ppm	^[33]
1986	6.67449(81)	120 ppm	^[34]
1998	6.673(10)	1500 ppm	^[35]
2002	6.6742(10)	150 ppm	^[36]
2006	6.67428(67)	100 ppm	^[37]
2010	6.67384(80)	120 ppm	^[38]
2014	6.67408(31)	46 ppm	^[39]
2018	6.67430(15)	22 ppm	^[40]
2022	6.67430(15)	22 ppm	^[41]

2007년 1월호 ''사이언스''에 실린 픽슬러 등의 논문에서는 원자 간섭계라는 새로운 기술을 이용하여 ''G'' = 6.693(34)×10⁻¹¹ m³⋅kg⁻¹⋅s⁻² 라는 값을 보고했다. 이는 당시(2006년) CODATA 값보다 0.28% (2800 ppm) 높은 값이었다.^[42] 로시 등이 개선된 냉원자 측정을 통해 2014년에 발표한 값은 ''G'' = 6.67191(99)×10⁻¹¹ m³⋅kg⁻¹⋅s⁻² 이었다.^[43]^[44] 이 결과는 기존의 권장 값에 훨씬 더 가까웠지만(픽슬러 등의 측정값에 오류가 있었음을 시사함), 2014년 CODATA 권장 값보다는 325 ppm 낮았으며, 표준 불확실도 구간이 서로 겹치지 않았다.

2018년 현재, 퀴니 등의 2013년 실험 반복을 포함하여 상충되는 측정 결과들을 재평가하려는 노력이 NIST 주관 하에 진행 중이다.^[45]

2018년 8월, 중국 연구팀은 두 가지 다른 방법을 사용한 비틀림 균형 실험을 통해 ''G'' = 6.674184(78)×10⁻¹¹ m³⋅kg⁻¹⋅s⁻² 와 ''G'' = 6.674484(78)×10⁻¹¹ m³⋅kg⁻¹⋅s⁻² 라는 새로운 측정값을 발표했다.^[46] 이 측정값들은 표준 불확실도가 12 ppm으로 당시까지 보고된 가장 정확한 값으로 주장되었다. 그러나 두 결과값의 차이가 2.7''σ''에 달해, 아직 설명되지 않은 오차 원인이 있을 수 있음을 시사한다.

만유인력 상수의 2018년 및 2022년 CODATA 권장 값은 다음과 같다.

:''G'' = 6.67430(15)×10⁻¹¹ m³⋅kg⁻¹⋅s⁻²^[48]^[41]

괄호 안의 숫자는 마지막 자릿수를 단위로 한 값의 표준 불확실성을 나타낸다. 이 상수는 질량이 각각 1kg인 두 물체가 1m 떨어져 있을 때 서로 끌어당기는 힘을 뉴턴(N) 단위로 나타낸 값과 같으며, 매우 작은 값이다. 예를 들어, 무게 중심이 서로 1m 떨어진 1톤(= 1000kg) 물체 두 개가 서로 끌어당기는 힘은 약 6.7×10⁻⁵ N인데, 이는 지구상에서 약 6.8mg 질량의 물체에 작용하는 중력과 비슷하다.

또한, 만유인력 상수를 디랙 상수(ħ)와 진공 중의 광속(c)으로 환산한 양은 다음과 같다.

:''G/ħc'' = 6.70883(15)×10⁻³⁹ (GeV/''c''²)⁻²^[49]

8. 한국의 관점

주어진 원본 소스(`source`) 내용이 비어 있어, '한국의 관점' 섹션에 대한 내용을 작성할 수 없다. 내용을 작성하려면 해당 섹션과 관련된 원본 자료가 필요하다.

참조

_[1] 웹사이트 University of Washington Big G Measurement http://asd.gsfc.nasa[...] Goddard Space Flight Center 2002-12-23
_[2] 서적 Fundamentals of Physics John Wiley & Sons, Limited 2007-09
_[3] 서적 "Einstein's General Theory of Relativity: With Modern Applications in Cosmology" https://books.google[...] Springer Science & Business Media
_[4] 논문 The Foundation of the General Theory of Relativity http://www.albertein[...]
_[5] 서적 Introduction to General Relativity https://archive.org/[...] McGraw-Hill
_[6] 논문 The Newtonian gravitational constant: recent measurements and related studies 1997
_[7] 서적 The Foundation of Reality: Fundamentality, Space, and Time https://books.google[...] Oxford University Press
_[8] 서적 Relativistic Celestial Mechanics of the Solar System https://books.google[...] John Wiley & Sons
_[9] 웹사이트 Astrodynamic Constants http://ssd.jpl.nasa.[...] NASA/JPL 2009-02-27
_[10] 웹사이트 Geocentric gravitational constant https://iau-a3.gitla[...] IAU Division I Working Group on Numerical Standards for Fundamental Astronomy 2021-06-24
_[11] 논문 A Commemoration of Maskelyne at Schiehallion 1985
_[12] 문서 "Sir Isaac Newton thought it probable, that the mean density of the earth might be five or six times as great as the density of water; and we have now found, by experiment, that it is very little less than what he had thought it to be: so much justness was even in the surmises of this wonderful man!" Hutton 1778
_[13] 서적 The Earth: its shape, size, weight and spin https://books.google[...] Cambridge 1913
_[14] 논문 An Account of the Calculations Made from the Survey and Measures Taken at Schehallien 1778
_[15] 문서 Boys 1894 https://books.google[...]
_[16] 문서 Experiments to Determine the Density of the Earth Philosophical Transactions of the Royal Society 1798
_[17] 문서 2014 CODATA value
_[18] 문서 Physics, the human adventure: from Copernicus to Einstein and beyond https://archive.org/[...] Rutgers University Press 2001
_[19] 서적 The Mean Density of the Earth https://archive.org/[...] Charles Griffin 1894
_[20] 문서 F. Reich, On the Repetition of the Cavendish Experiments for Determining the mean density of the Earth Philosophical Magazine 12: 283–284.
_[21] 문서 Mackenzie (1899), p. 125.
_[22] 문서 A.S. Mackenzie, The Laws of Gravitation (1899) https://archive.org/[...]
_[23] 서적 The mean density of the earth https://archive.org/[...] London 1894
_[24] 논문 On the Newtonian Constant of Gravitation The Royal Society 1895-01-01
_[25] 문서 Carl Braun, Denkschriften der k. Akad. d. Wiss. (Wien), math. u. naturwiss. Classe, 64 (1897).
_[26] 문서 Sagitov, M. U., "Current Status of Determinations of the Gravitational Constant and the Mass of the Earth", Soviet Astronomy, Vol. 13 (1970), 712–718, translated from Astronomicheskii Zhurnal Vol. 46, No. 4 (July–August 1969), 907–915 (table of historical experiments p. 715).
_[27] 문서 Mackenzie, A. Stanley, The laws of gravitation; memoirs by Newton, Bouguer and Cavendish, together with abstracts of other important memoirs https://archive.org/[...] American Book Company 1900
_[28] 논문 A redetermination of the constant of gravitation
_[29] 문서 P. R. Heyl and P. Chrzanowski (1942), cited after Sagitov (1969:715).
_[30] 논문 CODATA recommended values of the fundamental physical constants: 2002 http://www.atomwave.[...] 2006-07-01
_[31] 논문 CODATA recommended values of the fundamental physical constants: 2010 http://physics.nist.[...] 2012-11-13
_[32] 논문 Determination of e/h, Using Macroscopic Quantum Phase Coherence in Superconductors: Implications for Quantum Electrodynamics and the Fundamental Physical Constants American Physical Society (APS) 1969-07-01
_[33] 논문 The 1973 Least-Squares Adjustment of the Fundamental Constants AIP Publishing
_[34] 논문 The 1986 adjustment of the fundamental physical constants American Physical Society (APS) 1987-10-01
_[35] 논문 CODATA recommended values of the fundamental physical constants: 1998
_[36] 논문 CODATA recommended values of the fundamental physical constants: 2002
_[37] 논문 CODATA recommended values of the fundamental physical constants: 2006
_[38] 논문 CODATA Recommended Values of the Fundamental Physical Constants: 2010
_[39] 논문 CODATA Recommended Values of the Fundamental Physical Constants: 2014
_[40] 웹사이트 The 2018 CODATA Recommended Values of the Fundamental Physical Constants http://physics.nist.[...] 2019
_[41] citation Codata Internationally Recommended 2022 Values of the Fundamental Physical Constants https://www.nist.gov[...] 2024-05-08
_[42] 논문 Atom Interferometer Measurement of the Newtonian Constant of Gravity 2007-01-05
_[43] 논문 Precision measurement of the Newtonian gravitational constant using cold atoms http://www2.fisica.u[...] 2014-06-26
_[44] 논문 Fundamental constants: A cool way to measure big G https://www.nature.c[...] 2014-06-18
_[45] 논문 Invited Review Article: Measurements of the Newtonian constant of gravitation, G
_[46] 논문 Measurements of the gravitational constant using two independent methods
_[47] 논문 Constraining a Possible Variation of G with Type Ia Supernovae 2014-04-10
_[48] 문서 CODATA Value
_[49] 문서 CODATA Value
_[50] 문서 Mohr et al. (2012) p.1594, TABLE XLVIII.
_[51] 문서 Mohr et al. (2012) pp.1587-1591
_[52] 문서 Mohr et al. (2012) p.1583, FIG. 6.
_[53] 문서 Older values of the constants
_[54] 문서 1982年から2010までの主な測定結果については、Mohr et al. (2012) p.1567, TABLE XVII. が参考になる。
_[55] 문서 Cohen and Taylor
_[56] 논문 Determination of e/h, Using Macroscopic Quantum Phase Coherence in Superconductors: Implications for Quantum Electrodynamics and the Fundamental Physical Constants American Physical Society (APS) 1969-07-01
_[57] 논문 The 1973 Least‐Squares Adjustment of the Fundamental Constants AIP Publishing
_[58] 논문 The 1986 adjustment of the fundamental physical constants American Physical Society (APS) 1987-10-01
_[59] 논문 CODATA recommended values of the fundamental physical constants: 1998
_[60] 논문 CODATA recommended values of the fundamental physical constants: 2002
_[61] 논문 CODATA recommended values of the fundamental physical constants: 2006
_[62] 논문 CODATA Recommended Values of the Fundamental Physical Constants: 2010
_[63] 논문 CODATA Recommended Values of the Fundamental Physical Constants: 2014
_[64] 웹사이트 The 2018 CODATA Recommended Values of the Fundamental Physical Constants http://physics.nist.[...] 2019
_[65] 문서 『理科年表2009』
_[66] 문서 Astrodynamic Constants
_[67] 문서 Fixler, Foster, McGuirk, and Kasevich
_[68] 문서 Selected Astronomical Constants
_[69] 문서 Earth Fact Sheet
_[70] 논문 CODATA Recommended Values of the Fundamental Physical Constants: 2010 http://physics.nist.[...]
_[71] 저널 Experiments to determine the Density of the Earth